Cooking Pizza Without Preheating

One night at around 2 a.m. I couldn’t fall asleep and I was hungry so I cooked a pizza. Looking at the cooking directions, I set the temperature on the oven at 400°F and prepared to wait until the oven was done preheating before putting the pizza in and waiting the the recommended 8-10 minutes of cookings time. But… what if I ignored the recommended directions and put the pizza in and let it cook throughout the preheat process! For some reason I never thought of this before.

I’m not a stickler about the perfectly cooked pizza (especially at 2 a.m.) but I was curious, if I wanted to cook the pizza with the same amount of heat as the recommended directions but instead cook the pizza throughout the preheat process, how long should I leave the pizza in the oven?

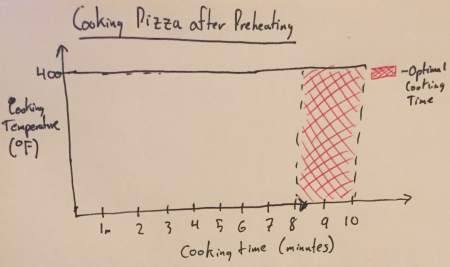
The graph below shows the optimal time to cook a pizza according to the directions given (cook at 400°F for 8-10 minutes):

The area under the curve to the 10-minute mark is 4,000°F•minutes or 240,000°F•seconds. That amount of heat flow (whose units are usually Joules • seconds) is the target heat for our preheat method. The goal is to cook our pizza so the heat flow from the other method is equal to the area in the graph above.

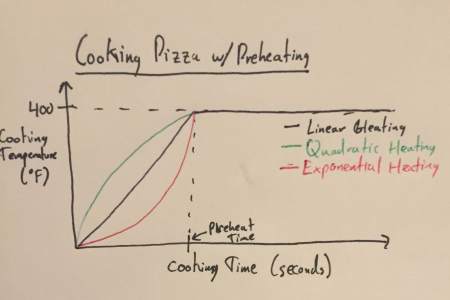
The graph below shows the possible heating trends the oven can take (Linear, Quadratic, and Exponential):

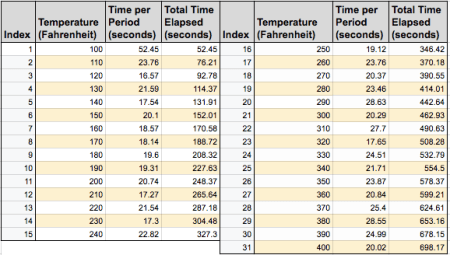
The next morning I woke up and timed the oven's preheating by 10°F increments (The oven, for reference, is a Whirlpool Gold Series that actually shows you the temperature its heating at) in order to test which trend the oven actually heats at. The data I took is in the table below:

The images below show the regression outputs for the linear, exponential, and quadratic models respectively:

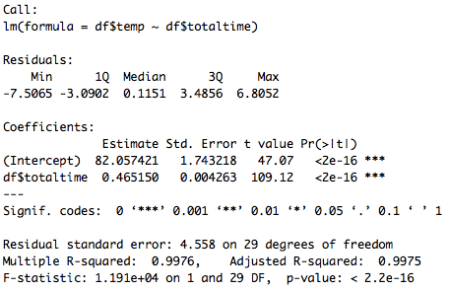
All of the coefficients of regressions from the three models are individually statistically significant at the 1% level. The F-statistics for the three models are also significant, but the R-squared values show the linear and quadratic models are the front runners for our final model (R-squared = 0.9975 and 0.9998 respectively). Using residual analysis, shown in the four graphs below, we choose the quadratic model in the end.

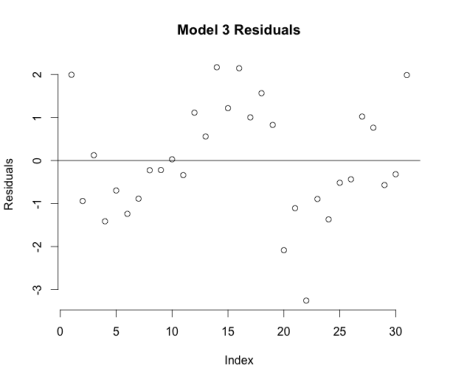
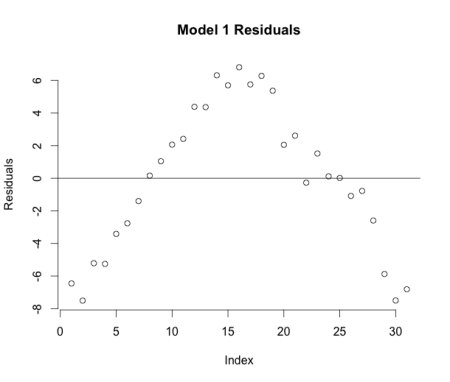
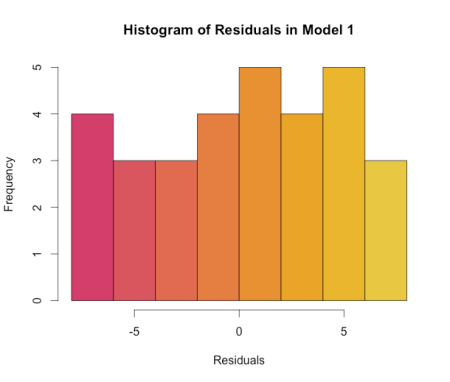
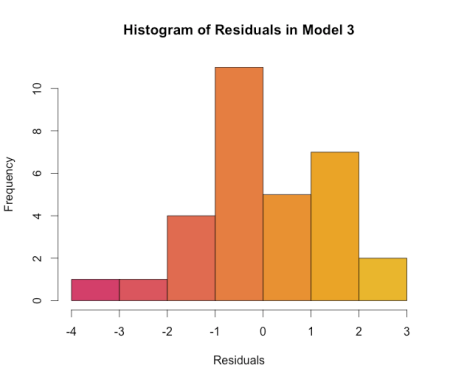
Model 1 clearly suffers from heteroskedasticity, misspecification, and the residuals are not normally distributed, which would cause the model to be biased. Model 3 obeys all of the OLS assumptions and is an incredibly descriptive model as 99.98 percent of the variation in temperature can be explained by variation in the dependent variables, total time and total time-squared. The final model is:

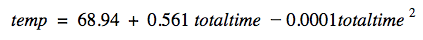
The intercept makes sense because if the oven is heated up for zero seconds it would be around room temperature, which is usually around 72°F. By plugging in 400°F into the regressand, we can find the amount of time it takes for the oven to finish preheating. Because its a quadratic equation we get two different answers: 671.9 seconds and 4,928.1 seconds. It's clear we want the first result but just to check we can do some quick calculus to find the critical value of the quadratic equation: 2,800 seconds. 671.9 is below that so we'll use that value. So far, our pizza cooking graph looks like this:

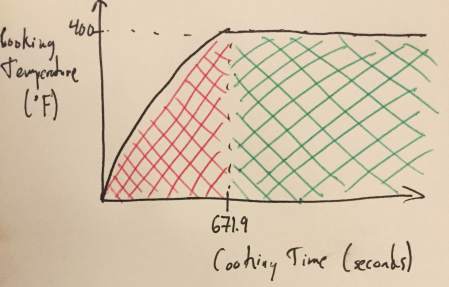
The red area represents the heat flow into the pizza during the preheat time. It can be calculated by computing the integral of the quadratic regression equation like so:

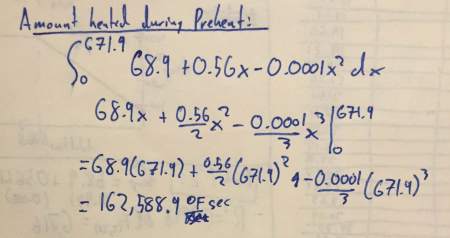
After preheating the pizza, we need a heat flow of 240,000°F•seconds - 162,588.9°F•seconds, which equals 77,411.1°F•seconds and is the green area from the last graph. The time left to cook the pizza to the recommended total heat flow is simply 77,411.1°F•seconds / 400°F, which equals 193.5 seconds or 3.2 minutes. In total, the preheat method of cooking the pizza takes 865.4 seconds or 14.4 minutes and the recommended method takes 1,271.9 seconds or 21.2 minutes which yields a difference of 6 minutes and 48 seconds. Yes, the difference between the two methods is only 6 minutes and 48 seconds for the same total heat flow but when it's 2 a.m. and you're hungry every second counts.